之前在这篇 subset 限制连接数量 里,简单总结了 SRE book 书里讲到的 subset 算法的基本原理和问题。
之前还在做 mesh 的时候,也曾经想把 subset 算法在公司内落地,无奈和同事一起分析了两个星期以后,认为 subset 的:
- 需要 paas 给每个 container 分配连续 id,且在下线时需要自动补漏,目前 k8s 其实并没有这种策略,给每个服务都做成 stateful-set 也不现实
- 发布时(公司内服务实例多的服务需要批量发布)会导致大量的连接 shuffle,进而导致服务的延迟变高
这两个问题对于很多服务,特别是涉及到公司核心链路的服务,本身就有严苛的 SLA 要求,如果因为 mesh 导致一发布就延迟上升,是不可接受的,所以难以落地。
最近 Google 在 acm queue 上发了一篇新文章:《Reinventing Backend Subsetting at Google》,详细地阐述了之前 SRE book 里写的那个 subset 算法的问题。
他们是在 Autopilot 这个项目落地的过程中遇到了阻力,这个叫 autopilot 的项目是帮业务模块自动做横向/纵向扩缩容的,对 subset 算法稍有了解的同学应该能想到,client 和 server 频繁的扩缩容会导致 subset 算法计算出的 subset 频繁发生变化,从而导致大量的连接 shuffle(在文章中里叫 connection churn)。
在 autopilot 落地之前,subset 算法在 Google 内部已经跑了 10 年了,但是因为连接 shuffle 会导致:
- 在途请求发生错误、延迟上升
- 因为大量连接重建,导致服务的 CPU/内存使用上升(好理解,因为 dial 的时候要分配资源)
- tcp slow start 会影响新创建的连接上的吞吐量,从而影响服务整体性能
- 连接缓存要承受更大压力
对于服务的影响随服务本身的性质不同而不同,有些延迟敏感的服务会导致服务的 SLO 受到影响,从而让 autopilot 的落地受阻。
这些问题在做 mesh 的时候我自己想了两个星期没有想到靠谱的解决方案,就放弃了,Google 的工程师则没有放弃。
根据 Hyrum 法则,只要能被观测到的行为都会被依赖,所以他们先是分析了一下以前的算法会有哪些行为,这次详细地介绍了当初他们怎么推导出的 deterministic subset。先是讲了 random subsetting 的问题:
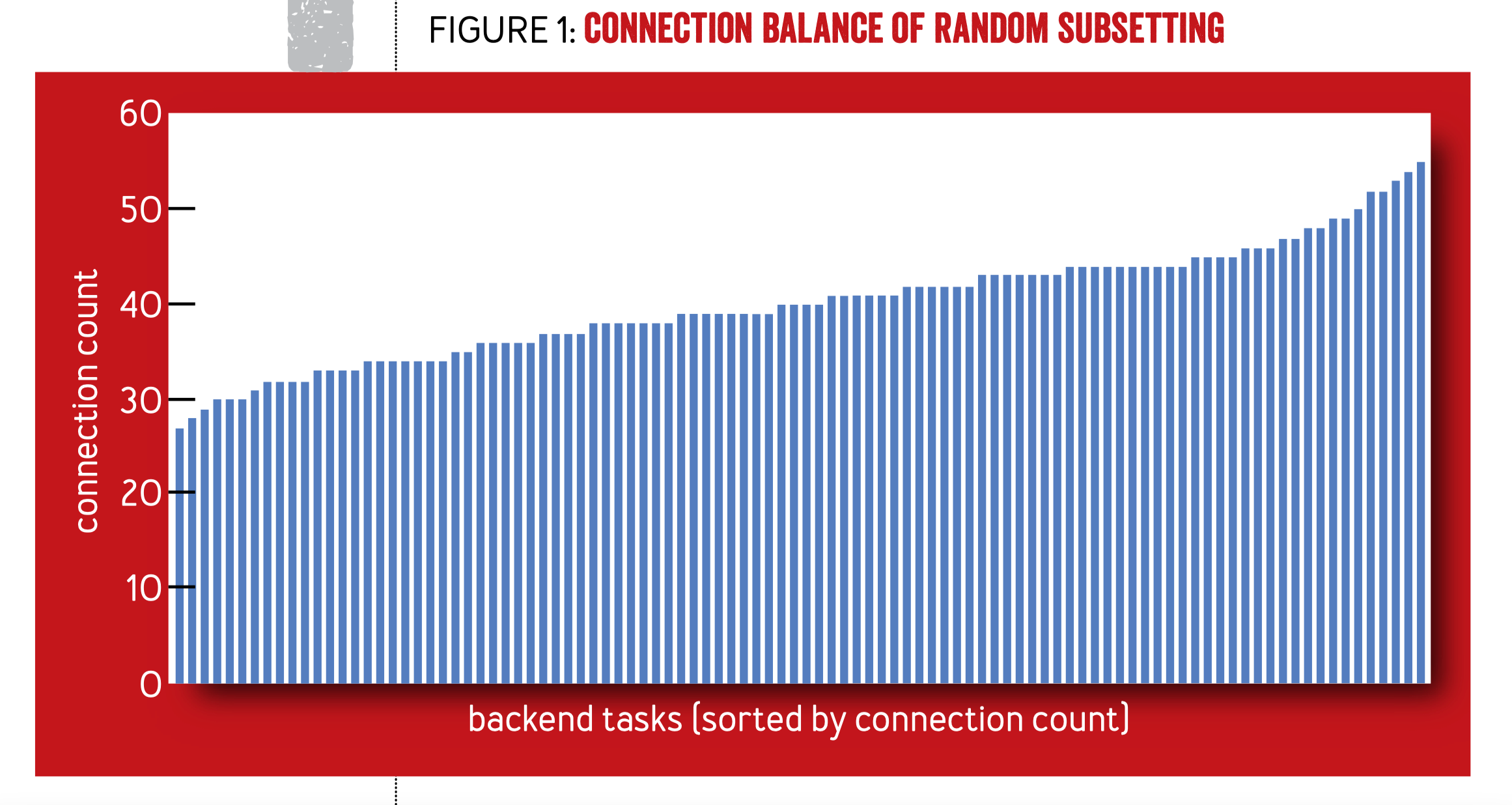
显然随机化的 subset 算法会导致连接不均匀,假设每一个请求的成本都相同,且每个连接上的请求速差不多,那么 server 端的这些连接数大致上和负载的关系就是正比关系。
后来 Google 想出了 deterministic subset 算法,因为之前在 subset 限制连接数量 里写过,这里就不在赘述了。
但是 deterministic subset 这个算法也有问题,在 client 或者 server 端的实例数量发生变化的时候,会导致大量的连接迁移和重建,比如下面这个例子:
后端的 size 从 10 变成了 11,就导致大量的 client 端的连接发生了迁移,上图中标红的是会发生变化的连接,不再使用的连接要断掉,新加入 subset 的 server 端要建新连接,可以看到 client 2 和 client 3 会有大量的连接重建。client 3 受的影响最严重,所有连接马上都不能用了。
为了解决这些问题,需要能够找到一种新算法,能解决之前的所有问题,要满足下面这些要求:
- 良好的连接平衡度
- subset 的 diversity 不能给一个 client 分配一堆连续的 server,要不批量发布的时候直接就跪了)
- 不能因为 client 端的重启导致大量连接 shuffle
- server 端重启时,对 client 端连接的 shuffle 影响应该尽量小,至少也是按后端数量来对前端产生影响(比如后端同一时刻重启了一半实例,那每个 client 端影响到一半的连接是可以接受的)
- subset 大小发生变化的时候,不能有大量连接 shuffle
- 更好的 subset 影响度
接下来文章就讲了工程师们重点考察的一些可能的算法。
consistent subsetting
然后 Google 的工程师先是想到了是否能用 consistent hashing 类似的搞法,做一个 consistent subset:

client 和 server 端都是按 consistent hash 的随机算法分布在环上的,蓝色的是 client,黄色的是 server。
然而这个算法并不会有较好的连接平衡度(server 端连接分布不均匀)和连接区分度(可能会把连续的实例分配给同一个 client)。
比如这张图里的 client 是蓝色的 0,它顺着 consistent subset 的环顺时针找,会用 3 和 2 两个连续的后端。这个不符合前面提出的 subset diversity。
Ringsteady subsetting
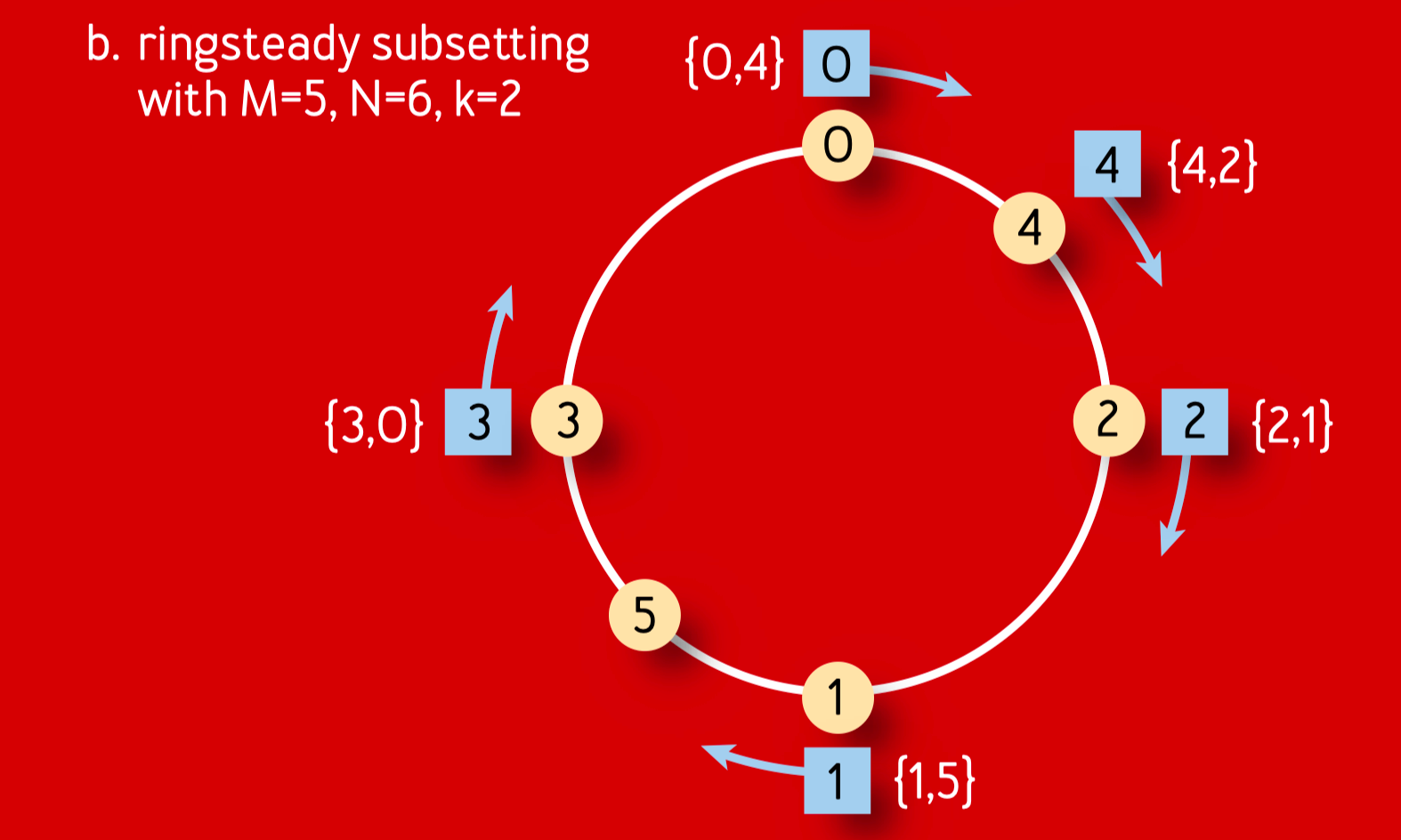
因为后端节点的分布要尽可能让后端变化时,前端和后端建立的连接也成相同比例变化,所以 Google 工程师选用了一个特殊的分布序列:binary van der Corput sequence。
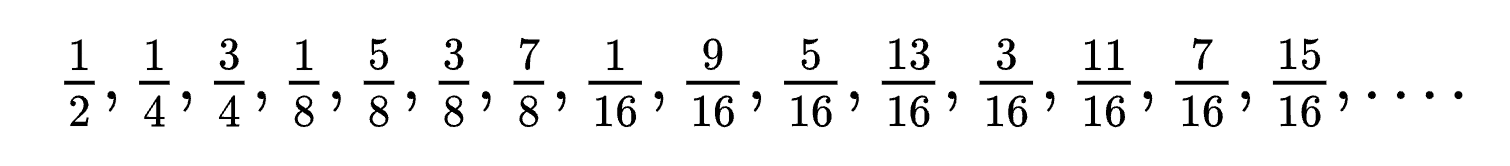
读者可以试着在圆环上摆一下每个节点,应该马上就能意识到这个序列的神奇之处了。
可以用下面的算法计算出相应的位置的值:
double corput(int n, int base){
double q=0, bk=(double)1/base;
while (n > 0) {
q += (n % base)*bk;
n /= base;
bk /= base;
}
return q;
}这个算法能保证较好的 subset diversity,subset spread,并且能均匀地将后端和前端节点分布在圆环上。
但它本身也有一些问题:
Frontend and backend scaling
client 端扩容叫 frontend scaling,server 端扩容叫 backend scaling。
ringsteady subsetting 的连接平衡度较差,比如下图的右边,当 client 的数量超过了 server 时,util 值没有趋近于理想值。
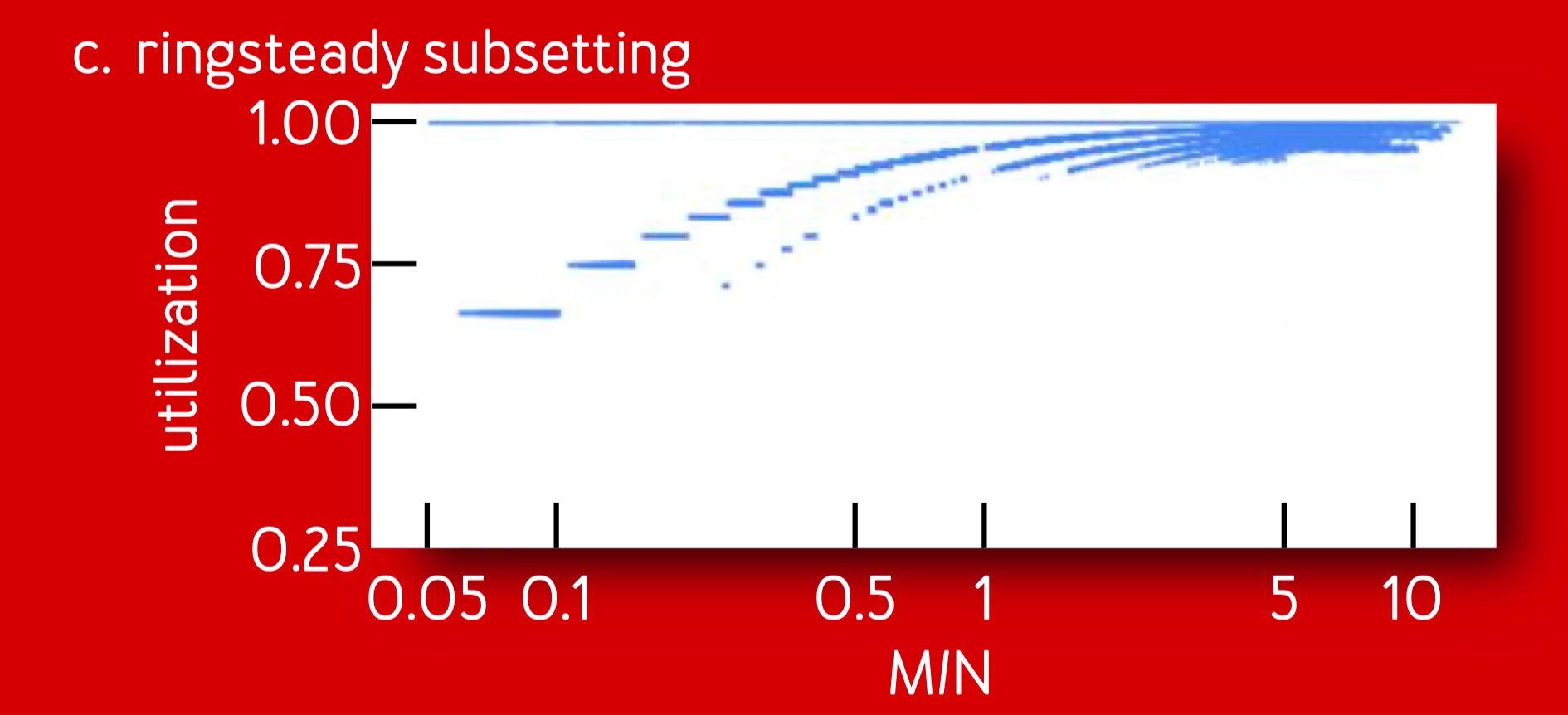
这和下图中的 determinisitic subsetting 有明显差距:
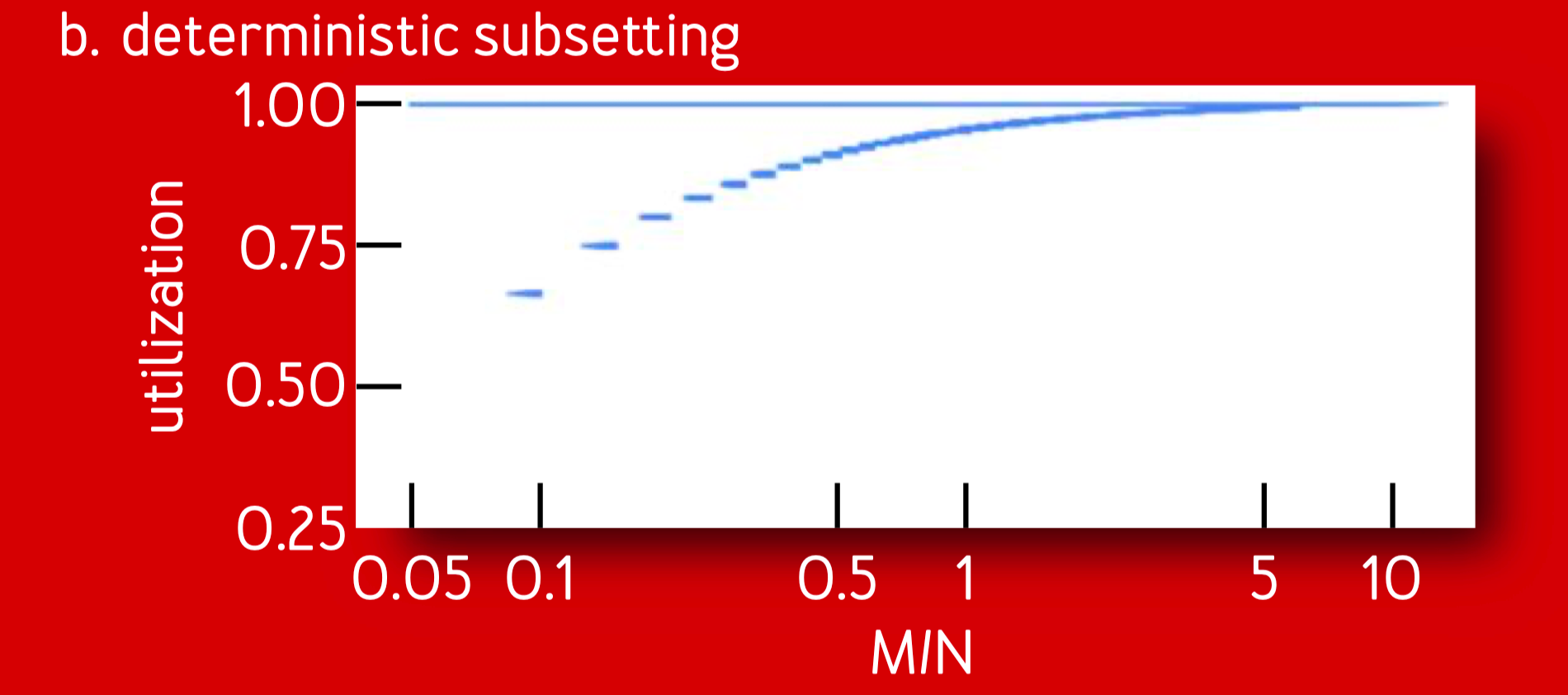
这里选用的低差异的序列,即前文的 binary van der Corput sequence 导致 client 和 server 在环上离得较近,而并不是按照距离来均匀分布。
如果把 server 和 client 端的数量一起纳入排序来在圆环上来做分布的话又会带来很多额外的困难,这里不再赘述了,感兴趣的同学可以去精读原文。
Rocksteadier subsetting
ringsteady subsetting 基本上能解决所有后端扩容的问题了,但是这个算法的 subset diversity 并不是很优秀,因为本质上它是 consistent subset 的一个变种,Google 的工程师还调研了一个叫 Rendezvous Hashing 的算法,不过结果也并不是很理想,因为没法很好得保证连接的平衡。
所以最后工程师想出了灵活组合 Ringsteady 来解决所有问题的算法,其流程如下:
- 将前后端所有实例进行分组:
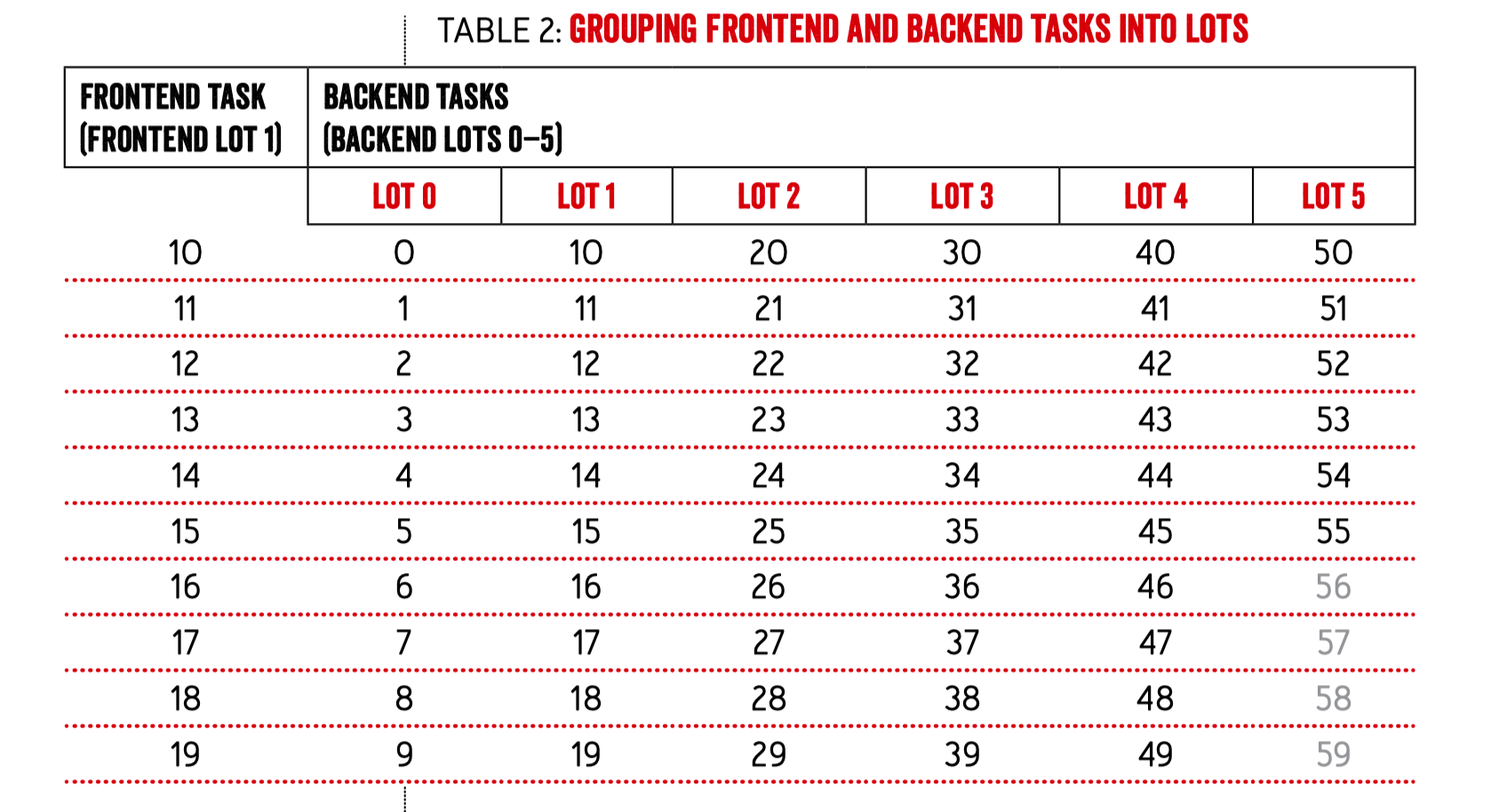
不足的组需要 padding,在表格中是 56-59。
然后将 server 端的分组内的实例进行 shuffle,这里需要保证每个 client 组内看到的 shuffle 结果是相同的,所以可以用 frontend 的 lot id 来作为伪随机算法的输入种子:
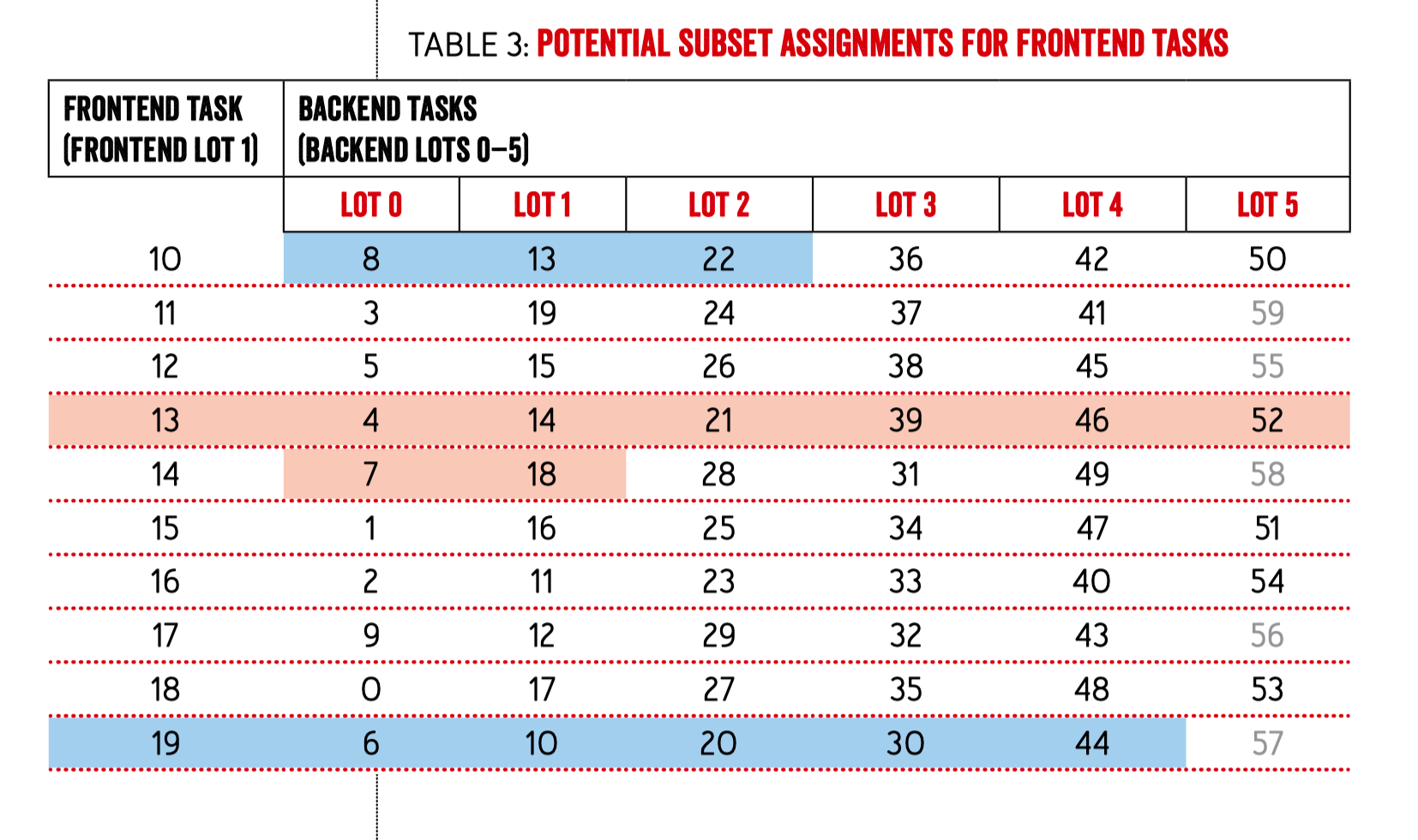
然后将 server 的 LOT 也就是组按照 ringsteady 的排序方式进行打乱:
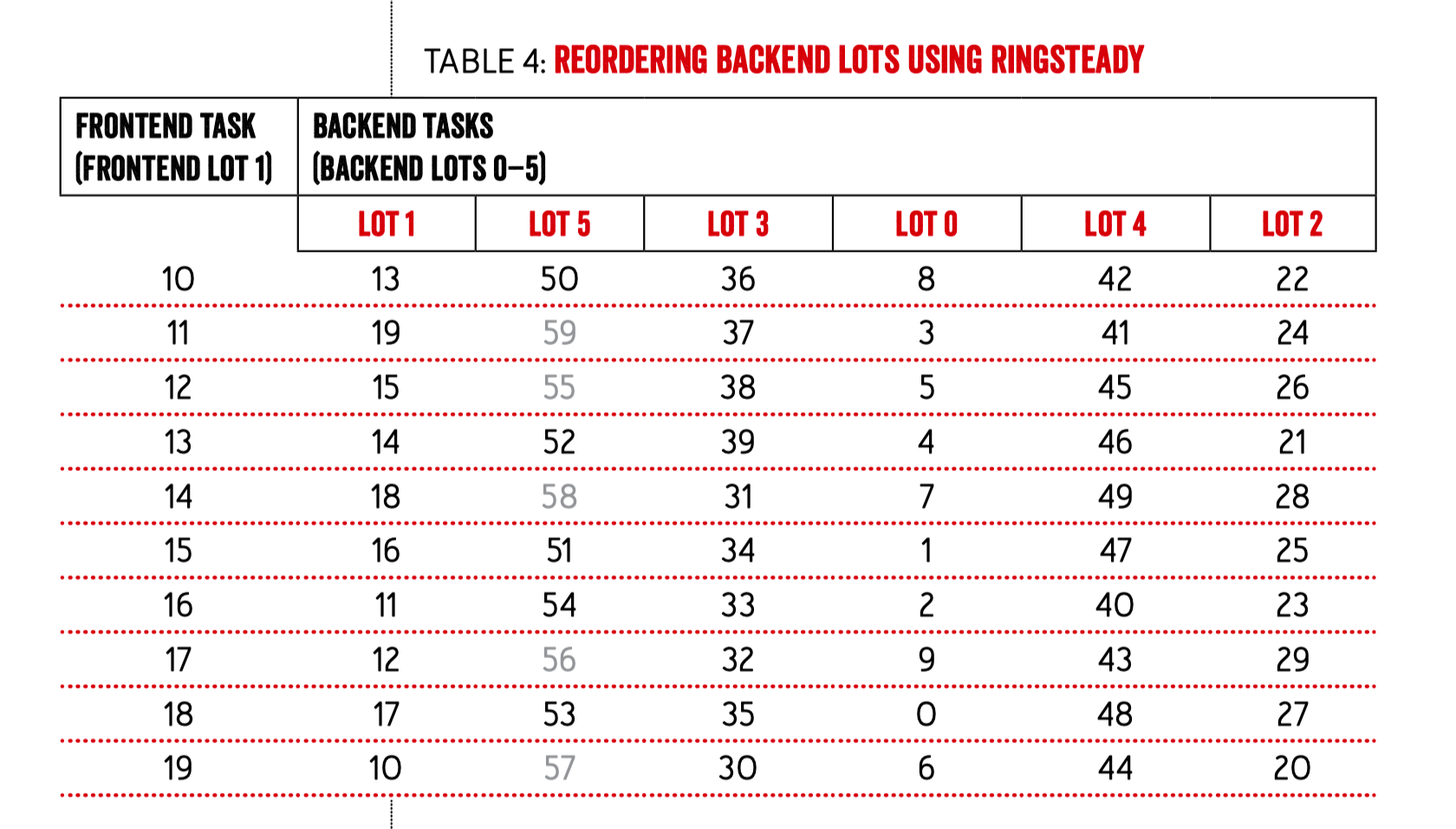
接着将同一组内的 client 也按照 ringsteady 的方式进行打乱:
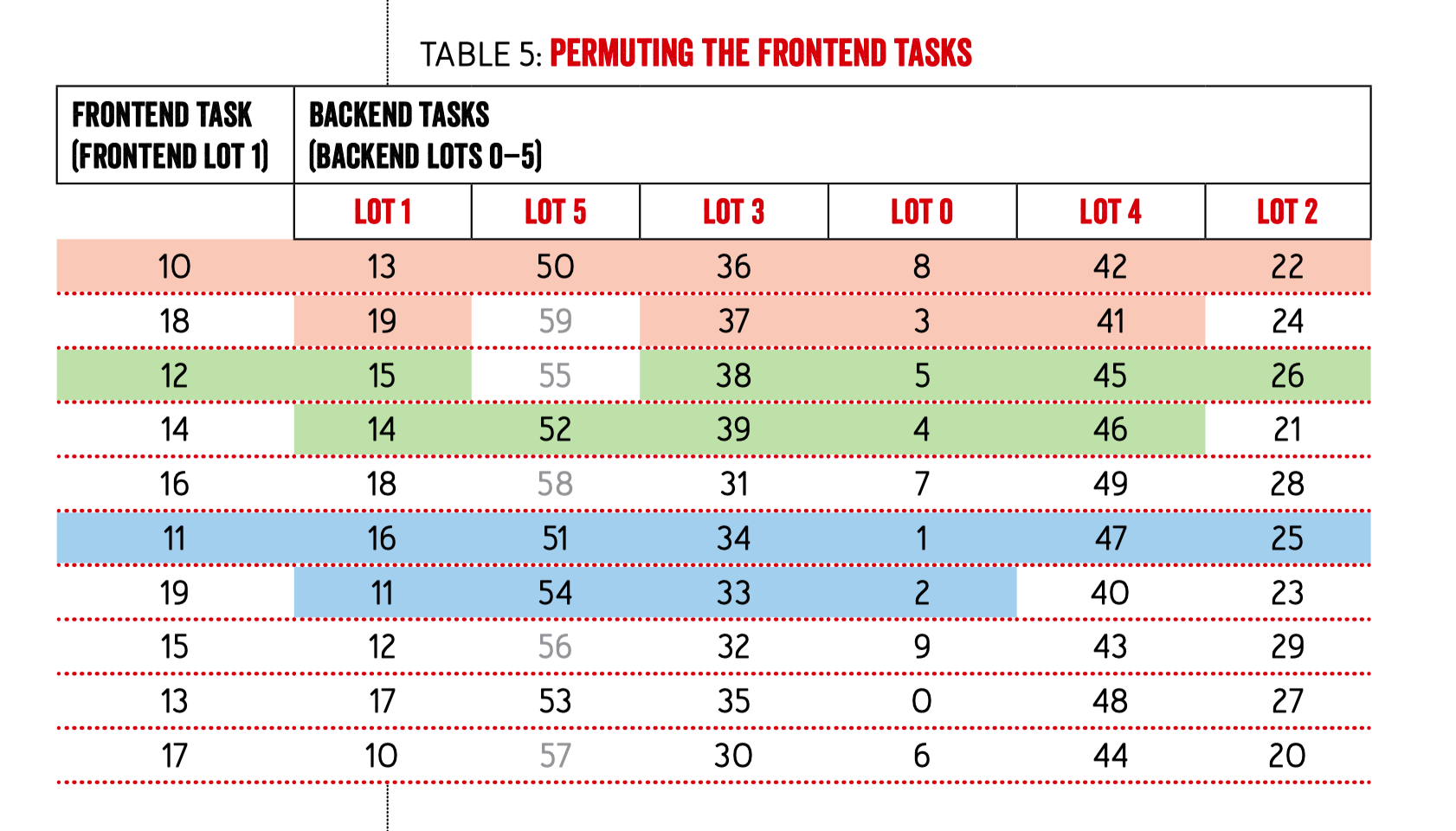
在上图中,我们每个 client 会向 server 端建 10 条连接,红色的表示的是 10 号 client 向 server 发起的连接,碰到之前 padding 进来的 server 实例 id 要跳过。绿色的表示的是 12 号 client 建立的连接,蓝色的表示的是 11 号 client 建立的连接。
到这里这个算法就结束了,在这篇文章里的分组大小 L 选择的是 10,增加分组大小的话可以增强算法的 subset diversity,但可能会导致连接的不均衡。幸运的是,一般比较小的连接数,比如 10 是能够提供较好的连接均匀度和 subset diversity 的。
这个算法部署到生产之后,再也没有发生过发布时大量的 connection shuffle,autopilot 也正常地铺开了,之后工程师们把这个 rocksteadier subsetting 作为默认的 subset 算法进行了上线,大多数业务的 owner 方对此也没有感知。
这个算法的思考过程困难重重,但最终的实现并不是特别困难,如果你的生产环境已经能够给所有服务分配连续 id 了,那么不妨现在就可以开始尝试了~
分配连续 id 是算法能成立的前提,别忘了。
这个算法可以在哪些场景落地
在文章开头我已经说过了,在 mesh 场景可以很好的落地。大多数 RPC 的连接建立过程也可以落地,对于 Go 这种网络编程模型,连接数对系统本身的内存占用影响会很大,选用文中的算法可以极大地节省长连接后端微服务的资源占用。
明年应该就能看到某些公司出来吹了。
